数学是自然科学的皇后，计算机的设计初衷是科学计算。计算机的最基本功能是需要存储整数、实数，及对整数和实数进行算术四则运算。

但是在计算机从业者的眼中，我们知道的数学相关的基本数据类型通常是整型、浮点型、布尔型。整型又分为int8（用8位表示的整数）、uint8（用8位表示的无符号整数）、int16、uint16、int32、uint32，浮点型又分为float16（半精度，FP16）、float32（单精度）、float64（双精度）。今天，我们就来聊聊浮点数。

#1 为什么叫浮点数？

由于实数在计算机中的表示方法是以小数点浮动的方式表示的，所以称之为浮点数。

1、计算机中的整数表示

众所周知，计算机最底层是二进制计数。用二进制数表示整数很简单（本文不考虑原码、反码、补码，也不考虑大端模式和小端模式），最高位表示符号位，0表示正数，1表示负数，余下的位表示二进制值。

int8即使用8位表示的整数，最高位用来表示正负符号，还有7位表示数字，其所能表示的范围是［-128，127］。有人可能会想，00000000表示正0，10000000表示负0，int8表示的范围岂不是［-128，127］吗？但用两个序列表示同一个数，这本身就是一种浪费。如果计算机从最底层就开始这样浪费，那还了得？所以节约资源，从我做起。

2、用定点数来表示实数

最高位表示符号，然后再约定整数占几位，余下的位都是小数。从另一个角度来说，即小数点的位置是固定的。优点是计算很方便，缺点是存储的数据范围有限。

3、用浮点数来表示实数

最高位表示符号，再约定一部分二进制位表示指数域，余下的是数域。优点是能表示的数据范围很大，缺点是计算慢。但是80286出现后，有了浮点协处理数（FPU），浮点数表示方式成为了主流。

IEEE-754是IEEE制定的二进制浮点数算术标准（IEEE即电气与电子工程师协会，这个协会制定了很多计算机领域的标准），也计算机中表示浮点数的行业标准，于1985年正式采用，2008年和2019年又分别进行了完善和修订。

我们以最常见的64位、32位、16位浮点数为例，如下图所示：

FP64称为双精度浮点数，一共64位，1位表示正负符号，11位表示指数，52位表示小数，可表达的精度范围是±2.23×10-308～±1.80×10+308；

FP32是我们最常用的浮点数，也称为单精度浮点数，一共32位，1位表示正负符号，8位表示指数，23位表示小数，可表达的精度范围是±1.18×10-38～±3.4×10+38；

FP16称为半精度浮点数，一共16位，1位表示正负符号，5位表示指数，10位表示小数，可表达的数据范围是±6.10×10-5～±65504。

计算方式：(-1)S×（20+M）×2E

S表示最高位符号位，为1表示负数，为0表示正数；M表示尾数域，最高位权重为2-1，次高位权重为2-2，依次递减；E表示指数域。

有如下几种情况：

• 当指数位全为0，尾数位全为0时，表示的就是0
• 当指数位全为0，尾数位不全为0时，表示为subnormal value，非规格化浮点数，是一个非常小的数
• 当指数位全为1，尾数位全为0时，表示的是无穷大。此时如果符号位为0，表示正无穷，符号位为1，表示负无穷
• 当指数位全为1，尾数位不全为0时，表示这不是一个数（做过深度学习训练的同学们可能会碰到这样的问题，在训练模型时，有时训练会因为运行过程出现了NaN(Not a Number,非数字)而导致训练过程被近停止）
• 其余情况下，指数位的值减去2n-1-1（n表示指数域的位数）就是其表示的指数

我们再以最简单的16位浮点数为例，如下图所示：

一共16位，最高位代表正负符号，接下来5位是指数域，最后10位是数域。其指数域的值是23+22-（25-1-1）=-3。尾数域是20+0×2-1+1×2-2+……，即最终其表示的数是2-3×（20+2-1）=2-3+2-4

同理，我们可以推导出16位浮点数可以表示的最大精度值：0 11110 1111111111

转换为十进制数：指数域为24+23+22+21-（25-1-1）=15，尾数域全为1，215×1.1111111111(b) = 215 × 1.9990234375(d) = 65504

16位浮点数可以表示的最小精度值（除了subnormal value）：0 00001 0000000000

转换为十进制数：指数域为20-（25-1-1）=-14，尾数域全为0，2-14×20约等于十进制的6.104×10-5=0.00006104

互联网上有一些很有意思的网页，能帮我们更深刻的认识到浮点数。我们挑选了由纽约市立大学计算机科学系提供的网页，网址为https://babbage.cs.qc.cuny.edu/ieee-754.old/decimal.html（或者也可以打开https://baseconvert.com/ieee-754-floating-point）。

接下来，我们随机输入一个浮点数，例如38.375，然后点击Rounded，再看看其在计算机中是如何表达的。

• 最高位是31位（位序从0开始），此处为0，表示是正数
• 接下来是指数域，从30位到23位一共是8位，最大能表示的数是256，最小能表示的数是0
• 指数域的值要减掉127，此处指数域是10000100，即132-127=5
• 余下的都是尾数域，从22位到0位一共是23位，此处是1.00110011（小数点前面的1是最终的32位数据里不存在的，因为尾数规范化后都是以1开始，所以这个1都是省略的）

最高位好理解，但是指数域5和尾数域的1.00110011是怎么得到38.375的？请各位先思考一下再看下面的计算过程。

1.00110011=1×20+0×2-1+0×2-2+1×2-3+1×2-4+0×2-5+0×2-6+1×2-7+1×2-8（=1.19921875）

1.19921875×25=38.375

或者直接将数域的小数点往后移五位，得到：

1×25+0×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+1×2-3=38.375

移动数域的小数点位置，这个操作是不是浮点？我认为，这就是浮点数的由来。

接下来还有一个很有意思的问题，即浮点数的精度问题。以0.3这个数为例，我们输入0.3后，分别点击Not Rounded和Rounded（因为这里是二进制数，不适合翻译为四舍五入，所以我用原单词替代），分别得到如下两图：

Not Rounded模式下

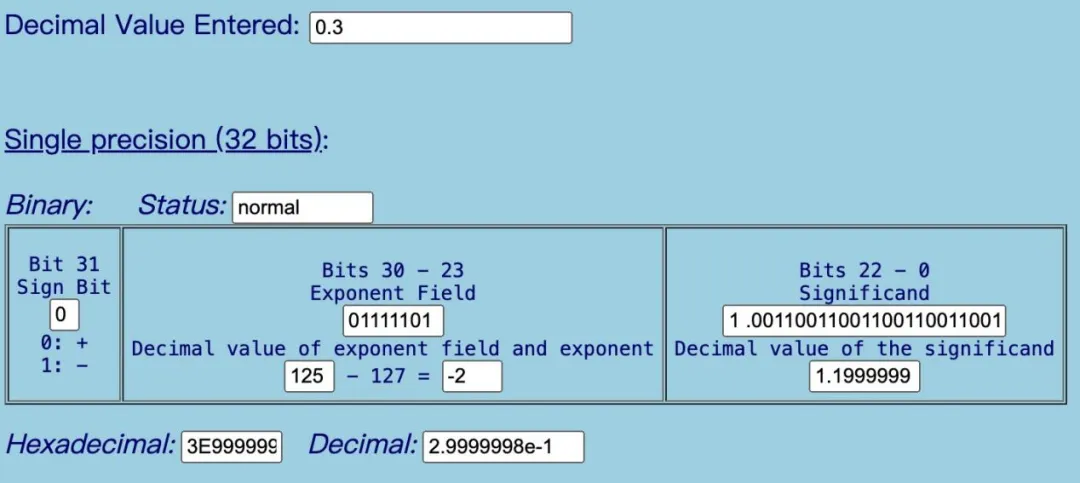
Not Rounded模式下，数域为1 .00110011001100110011001，最终计算得到的十进制数是0.299999总是比0.3小一点点。

为什么会这样？因为十进制的有穷数0.3，转换为二进制数后是一个无穷数（1001无限循环），如果直接扔掉后面的数，那么最终转换后的十进制数据就会少了一点点，变成了0.29999999。

Rounded模式下

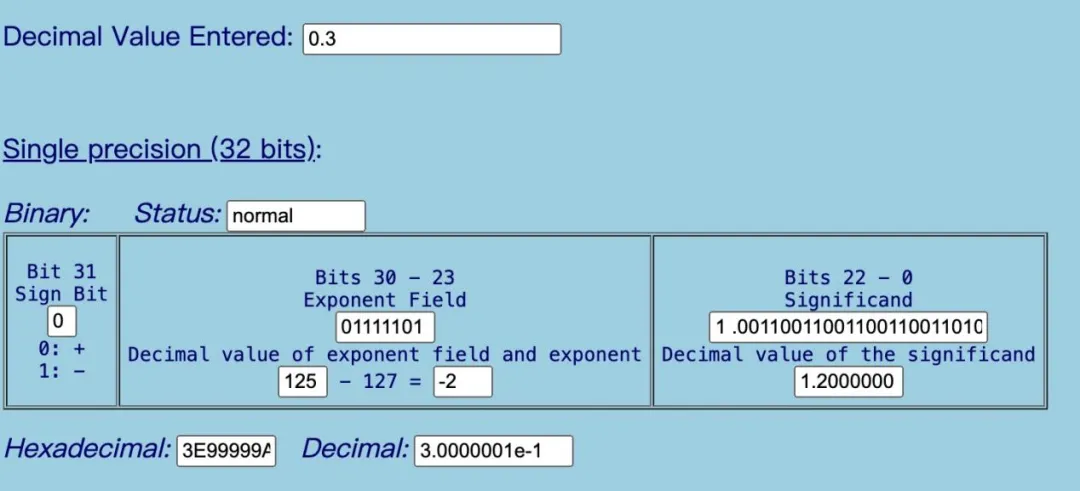
Rounded模式下，数域为1 .00110011001100110011010，也就是向前进了一位，这样最终得到的数变成了0.30000001，即比实际的十进制数0.3大了一点点。

所以在实际编程中，不建议对浮点数数据直接进行等值比较，一般使用区域比较，因为浮点数存在精度问题。c/c++程序员们遇到的问题0.1 + 0.2 = 0.30000000000000004也是这个原因导致的。

#2 BF16(Brain Float)

BF16是一种全新的浮点数格式，专门服务于人工智能和深度学习，最开始是Google Brain发明并应用在TPU上的，后来Intel，Arm及一众头部公司都在广泛使用。

BF16也是用16位来表示浮点数，但是是用8位表示指数，用7位表示小数，此时BF16表示的整数范围和FP32是一样的，小数部分则存在着很大的误差。

以前大部分的AI训练都使用FP32，但有相关的论文证明，在深度学习中降低数字的精度可以减少tensor相乘所带来的运算功耗，且对结果的影响却并不是非常大，且更少的尾数也使它能够拥有更小的芯片面积。因此在模型越来越大、计算越来越密集的人工智能领域，BF16也得到了广泛的应用。

#3 模型量化及INT8

从数据在计算机上的表示来看，整数运算比浮点数运算要快很多。而训练一个深度神经网络模型得到的参数通常都是FP32类型的，我们将其部署到终端NPU上时，通常需要将其量化为8位整数（即int8或者uint8）。

为什么人工神经网络模型要量化？因为终端的算力、资源都是有限的，量化后有如下好处：

• 减小了模型尺寸。原有的一个参数如果是32位表示的实数，量化后用8位整数来表示，这样模型能缩小至原模型大小的四分之一；
• 降低了内存和存储占用；
• 降低了功耗；
• 提升了计算速度。